こんにちは！トイロジックでテクニカルアーティストをやっているトリと申します。普段はシェーダ制作をメインに据えつつ、ツールの制作やワークフローの構築なども担当しています。

今回は、「インテリアマッピング」の基礎について、HoudiniとUEマテリアルでの実例を交えながら解説してみようと思います！　なお筆者はHoudiniの初心者であり、内容に誤りが含まれている可能性がある事をあらかじめご了承ください。
使用バージョンは、UE4.27.2、Houdini19.5.640となります。

※ 文章が長くなりすぎたので、前後編に分けています。後編はコチラ。

前書き

インテリアマッピングとは

インテリアマッピング（Interior Mapping）とは、シェーダを使って、ビルの外から室内を覗いたような見た目を描く技術です。モデリングをすることなく部屋の一つ一つの奥行きを描くことができるので、低コストでリアリティを上げることができ、とても便利です。「Marvel’s Spider-Man」あたりから有名になった気がします。
 

この記事を書いたきっかけ

現在参加しているプロジェクトで使いたいという要望があり、検証をしたのがきっかけです。実はインテリアマッピング自体は以前にも扱ったことがあったのですが、その時はほぼ写経しただけで理屈の理解には至っていませんでした。今回はイチから学び直したので、せっかくなら、ということでブログ記事にしてみた次第です。

インテリアマッピングを勉強する上では、以下のページを大いに参考にさせていただきました。素晴らしい記事をありがとうございます！
インテリアマッピング(interior mapping)～１ｍ³距離編～ – コポうぇぶろぐ

なぜHoudini？

近頃、ちょっと複雑なシェーダを作る際には、Houdiniで計算を可視化する、ということをよくやるようになりました。

1. @Pとか@Nとかのアトリビュートを使うことで頂点ごと（≒ピクセルごと）の計算結果を可視化できる
2. 割と簡単にベクトルの計算ができる

といった強みがあるので、シェーダの計算を矢印とか使って3次元的に可視化するのにはもってこいなんですよね。今回のインテリアマッピングも、調べていくと視線ベクトルというベクトルをどう料理するか、というのが核のようだったので学ぶ上でHoudiniで可視化するのは相性がよさそうだと思い、取り入れてみました。

やってみようインテリアマッピング　～とりあえず各面の座標まで出してみる

事前準備

描きたいもののイメージを明確にしよう

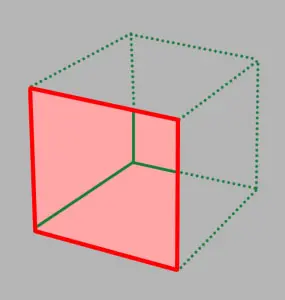
インテリアマッピングというと、ビルの窓から複数の部屋が見えるような見た目を想像すると思いますが、今回は基礎の基礎、ということで、正方形の平面（Plane）の中に、1つの部屋があるかのように見える、という状態を目指します。

言い換えると、Planeを手前の面とする立方体があって、それより奥に残りの5面がそれぞれあり、その立方体の内側だけがPlane越しに見えているという感じでしょうか。この、「Planeが立方体の手前の面」というのは割と重要な部分になってくるので、押さえておきましょう。

視線ベクトルについて

さて、「Planeの中に、1つの部屋があるかのように見える」というのがゴールであるとしました。ここにたどり着く上で基本となるのが、視線ベクトルを使った考え方になります。

ここで言う視線ベクトルとは、Planeの各ピクセルからカメラの逆の方向に伸びる正規化ベクトル、であると思ってください。2次元にすると下の図のような感じですね。要するにUEマテリアルの「CameraVectorノード」の逆ベクトルです。

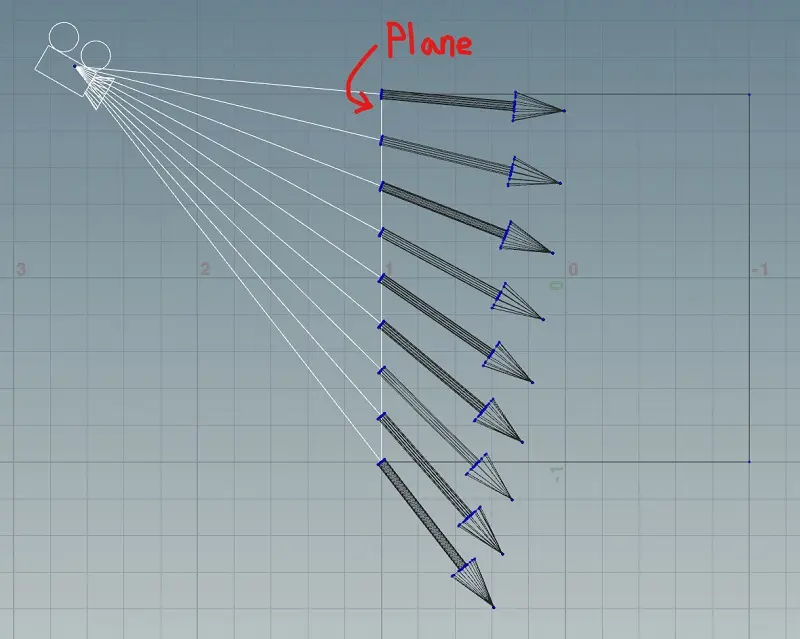
この視線ベクトルをUEで作る場合、

CameraVector * (-1)

でもいいですし、

normalize(WorldPosition-CameraPosition)

でもいいです。では、具体的な考え方を見ていきましょう。

考え方

根っこの考え方としては割と簡単で、各ピクセルの視線ベクトルを、立方体の各面にぶつかるまで伸ばしていく。ただそれだけです。面にぶつかって、伸びるのが止まった矢印を隙間なく並べていけば、立方体の形が再現される…というわけですね。

これを計算式にすると、

仮想の部屋の座標 = 視線開始座標 + 視線ベクトル * 視線ベクトルが立方体の各面のいずれかに衝突する距離

となります。

視線ベクトルは前項の通りとして、視線開始座標、は要するにPlane上の視線ベクトルの始点のことです。ややこしい計算が必要なのは、衝突する距離を求める部分です。逆に言えばここさえわかってしまえばインテリアマッピングの殆どは理解できたと言えるでしょう。

前提条件を決める

実際に詳しく実装を考えていく前に、前提条件を確認しておきます。

• インテリアマッピングを描画するPlane
  • +X方向を向いている
  • 中心は (1,0,0) である
  • サイズは2×2であると考える
• インテリアマッピングで描かれる仮想の部屋
  • 中心は (0,0,0)
  • サイズは2x2x2（各軸-1~1の範囲）
  • 回転はしていない

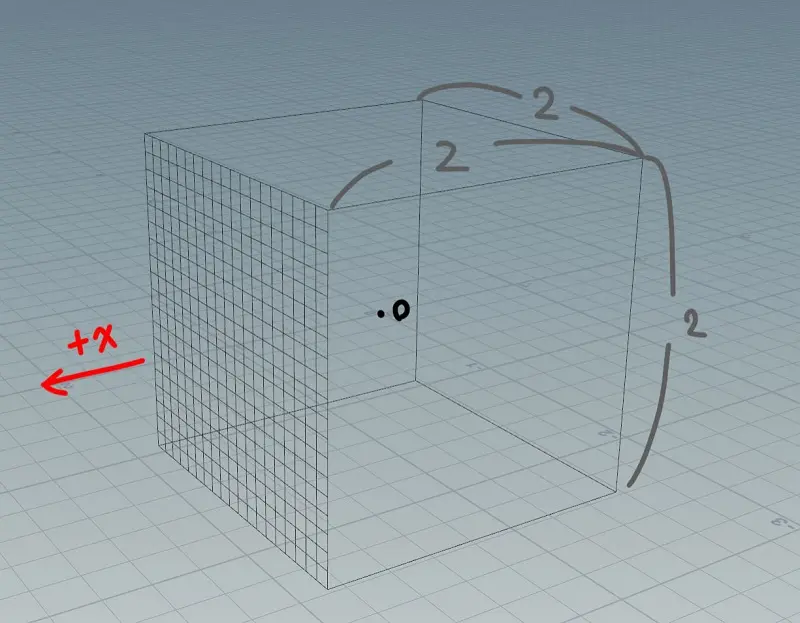
これらの前提条件は、インテリアマッピングを実現する上で必ずしも必須の条件ではありませんが、こうしておいた方が説明しやすいことと、サイズなどについては一貫性を持たせないと正しく表示されなくなる、などの都合から設定しています。以降は、この前提に基づいて説明していきます。

いざ実践

Planeの中心から各面までの距離を測る

では、インテリアマッピングのキモである、「視線ベクトルが立方体の各面のいずれかに衝突する距離」を求める方法を考えていきます。なお、以降、視線ベクトルはrayと呼称します。まずはシンプルに (1,0,0) の地点、つまりPlaneの中心のrayで考えてみましょう。

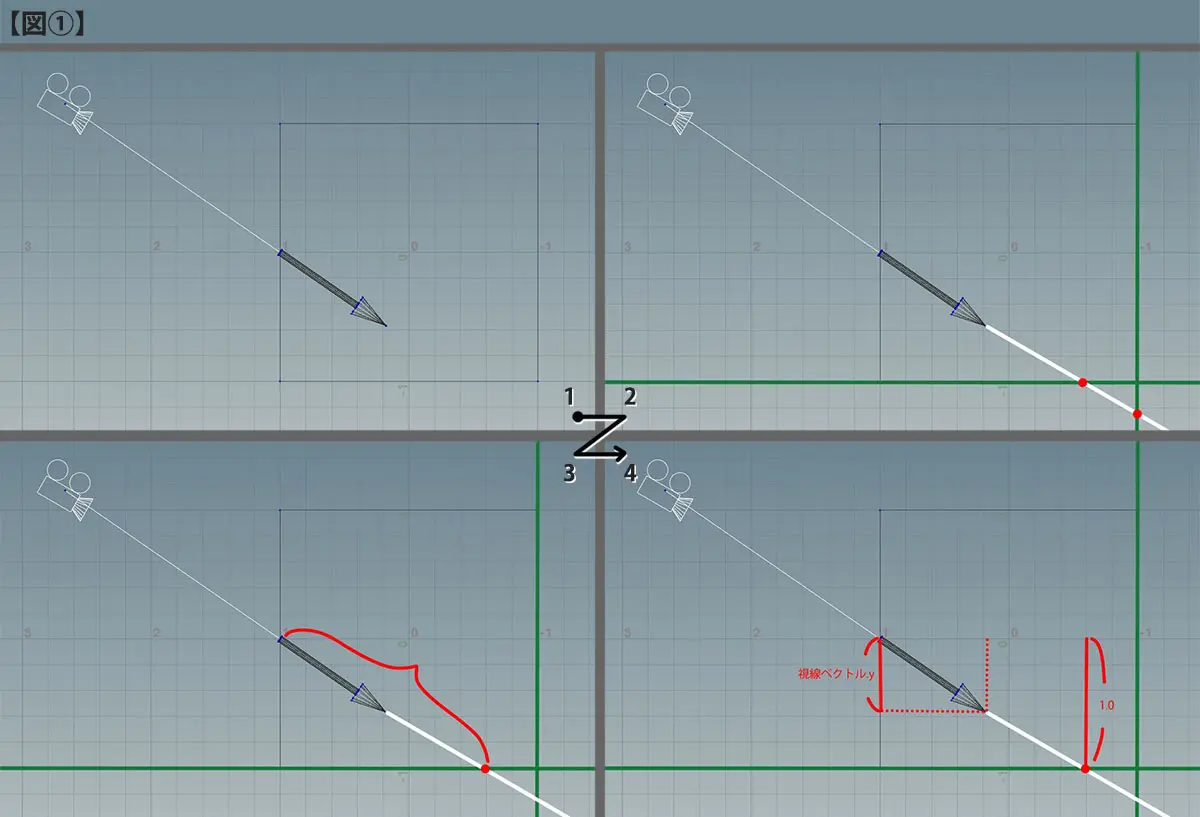
Planeの真横（Houdiniの＋Z側）から見た場合、図①-1のような状態ですね。現時点では立方体の形状は誰からも定義されていないので、とりあえず各面は無限に伸びていっていると考えます。この状態のrayが伸びていった先でぶつかる可能性があるのは、立方体の下の面と奥（図だと右側）の無限平面です。

図①-2の赤い点がぶつかる場所です。この時、下の面にぶつかるまでの距離を図で表すと、図①-3のようになります。この距離を求めるにはどうすればよいでしょう？ここで、距離が分かっている部分を確認してみます。図①-4を見てください。

まず、下の面のY座標（UEではZ座標と読み替えてください）は、立方体についての前提条件から、-1.0 となります。なので、rayの始点 (1,0,0) から下の面のY座標までの距離は

|(-1.0)-(0.0)| = 1.0

です。

また、rayの値は

normalize(WorldPosition-CameraPosition)

で既知です。

そのため、ベクトルの終点のY座標はそのまま

ray.y =  normalize(WorldPosition-CameraPosition).y

という風に持ってくることができます。

さらに、rayは正規化されているので、長さが1.0です。
この時、求めたい距離をaと置くと…

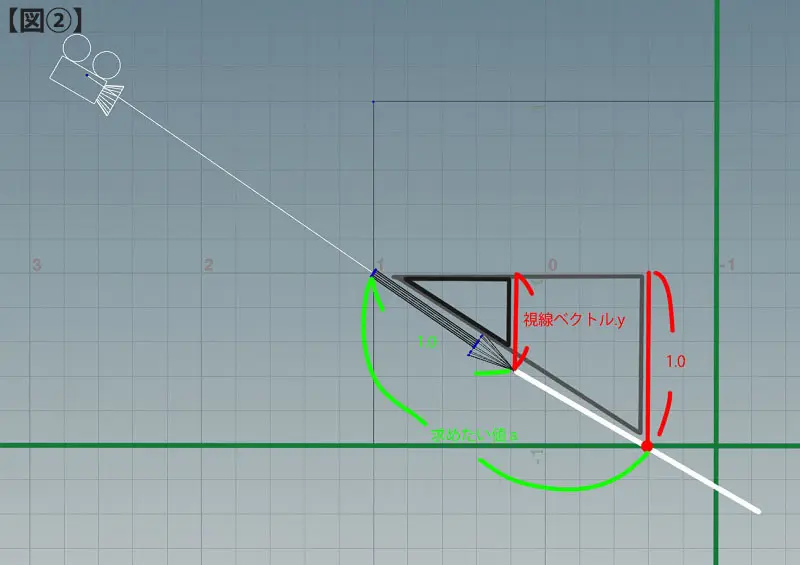
大きい三角形と小さい三角形が相似な図形であるので、

1.0 : a = ray.y : 1.0

これを変形すると

a * ray.y = 1.0

さらに変形すると

a = 1.0 / ray.y

となり、下の面にぶつかるまでの距離を求めることができました。同様に、奥の面にぶつかるまでの距離を求める場合は、下図のようになります。

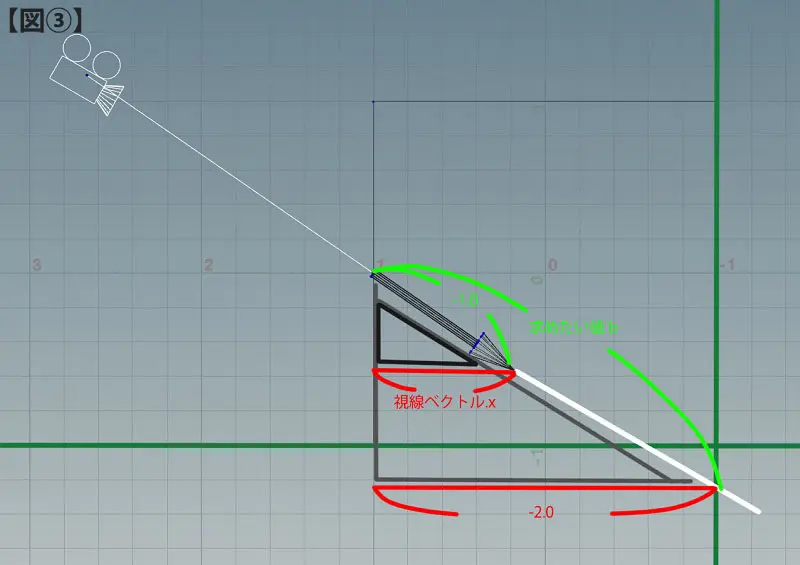
奥の平面のX座標が -1.0 なのに対し、今回の条件ではrayの始点のX座標は1.0となるので、

|(-1.0)-(1.0)|=2.0

がrayの始点からの距離になる点に注意してください。
式は、

b = 2.0 /ray.x

となり、こちらも求めることができました。

測った距離を元に描画する面を決める

前項までで各面にぶつかるまでの距離がわかったので、次にどちらがより近いかを判定し、
それにより手前の面だけ描画することを考えていきます。つまり、より距離の値が小さい方の値を返し、rayをその長さに伸ばせばよいということになります。より小さい値を返す、ということで、ここはシンプルにmin関数を使えます。

下の面までの距離 =  1.0 / ray.y
奥の面までの距離 =  2.0 /ray.x

なので、結果としては、

min((2.0 /ray.x), (1.0 / ray.y)) 

となります。

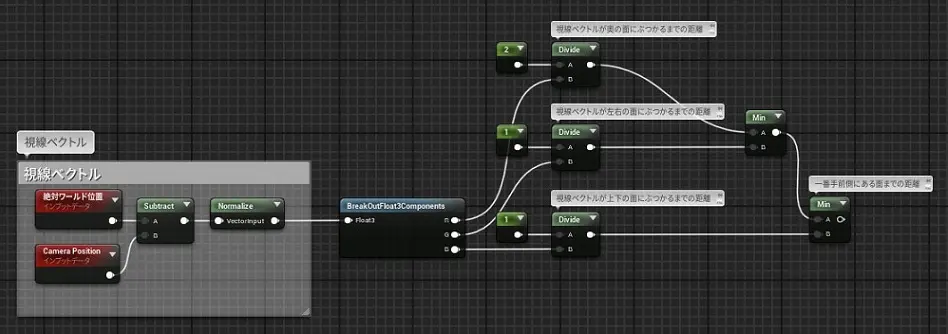
UEのシェーダノードで組む場合、ここまでの内容はこのようになります。（3次元なのでZ成分も含んでいます）

また、ここまでの内容を、Houdiniで2次元に限定して可視化してみると、以下のようになりました。

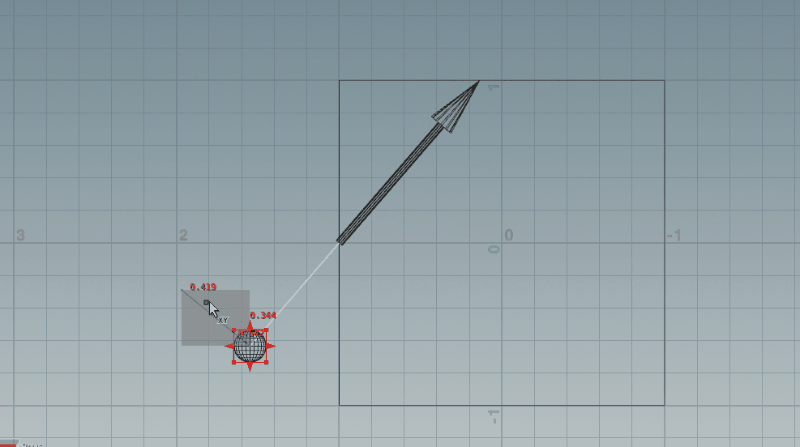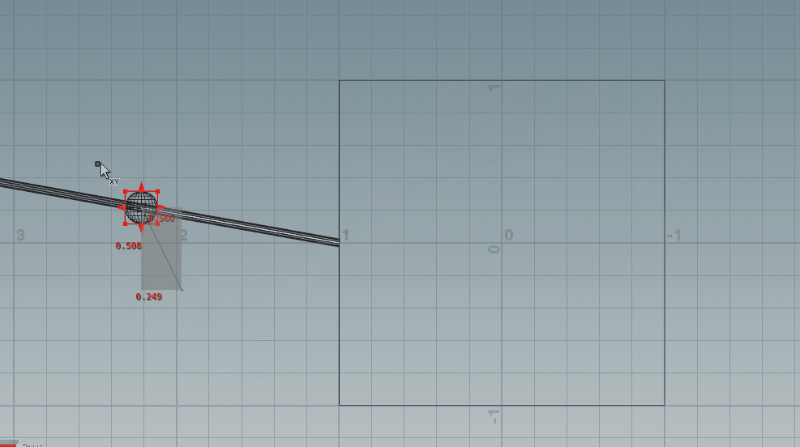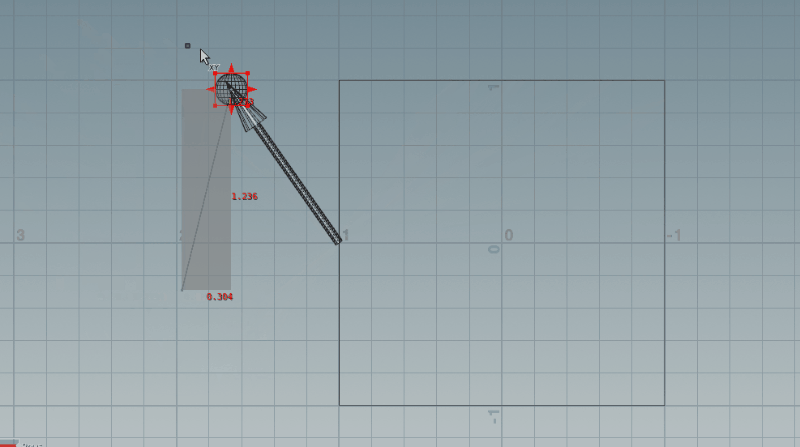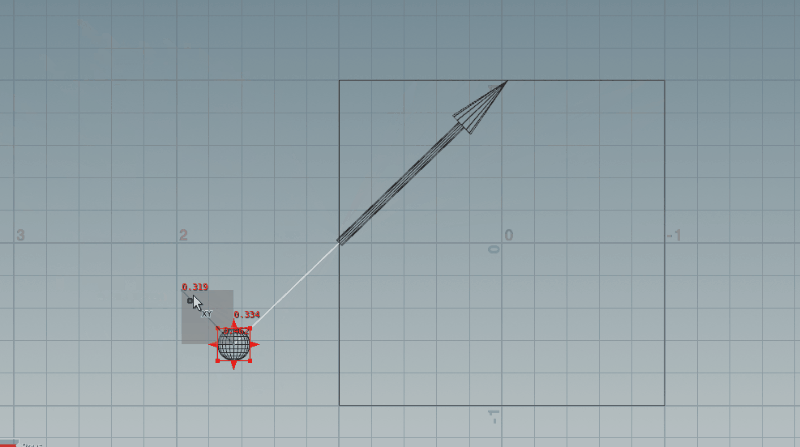
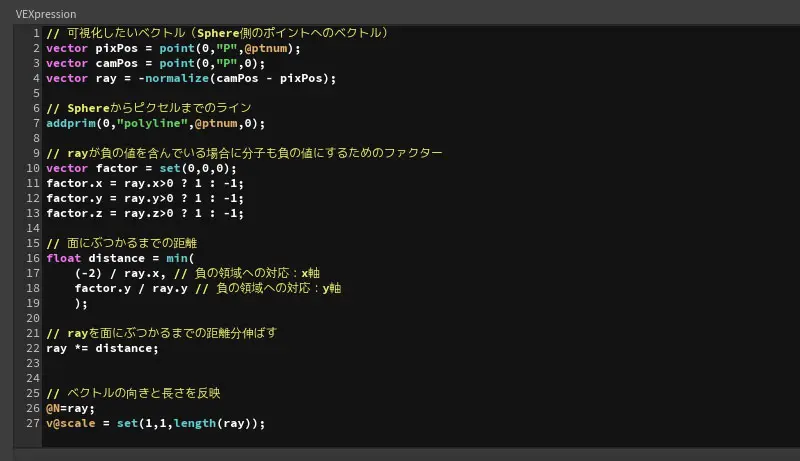
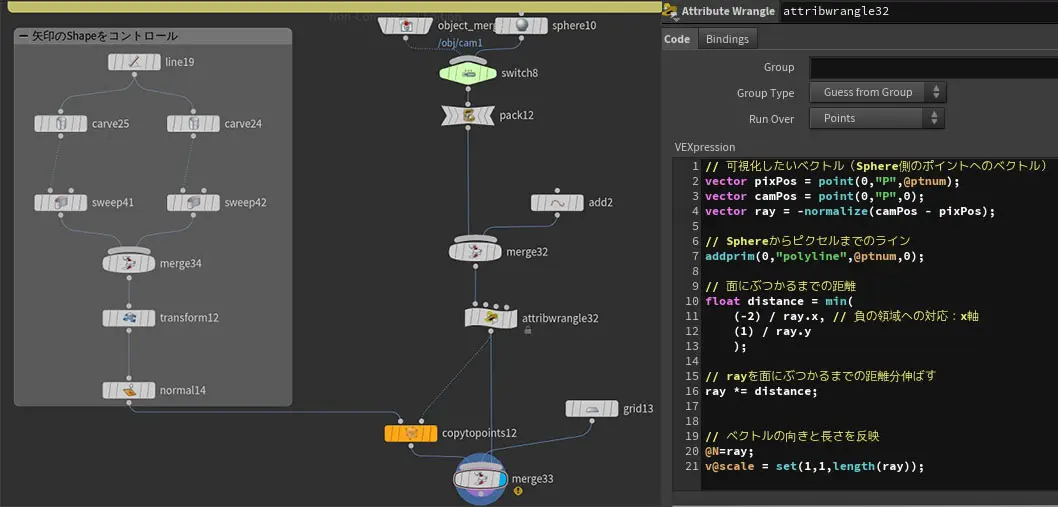
SOPネットワークはとVEXは次の画像の通りです。（イメージしやすくするためにちょっとだけ次の項の内容も含めて組んでいます）

カメラ（ここではSphere）が下の方にあるときは正しそうですね！ただ、カメラが上の方になるときには視線ベクトルが逆側を向いてしまっています。これは、矢印の長さに乗じる値が負の値になることで、視線ベクトルが逆方向にスケールされてしまっているからです。次はここを修正していきましょう。

負の領域も考慮する

前項で、矢印の長さに乗じる値が負になるとき、うまくいかない状況である、ということが分かりました。そもそもrayが今向いている方向に向かって伸びてほしいのですから、マイナス側へのスケールが望ましくないのは自明です。
ということで min((2.0 /ray.x), (1.0 / ray.y)) が常に正の値になるように修正していきます。

この min((2.0 /ray.x), (1.0 / ray.y)) が負になってしまうのは、rayのxyzいずれかの成分が負の場合です。どれかが負になってしまうと、割り算の商も負になり、負の値は正より当然小さいのでminの結果も負になります。

これを避けるには、rayのいずれかの成分が負になったとき、割り算の分子側も負に置き換わるように計算を変えてやればよいです。なのでまず、VEXの 1.0 / ray.y の部分を、以下のように書き換えます。

vector factor = set(0,0,0);
factor.y = ray.y > 0 ? 1 : -1;
flaot distance = min( 2 / ray.x, factor.y / ray.y);

一方で奥の面 ((-2) / ray.x) に対してはちょっと扱いを変える必要があります。これは、今回の前提条件だとrayは常に-X方向を向いていて、ray.xが正となり得ないからです。
なので、2.0 /ray.x　の分子を単純に負数に変えて、-2.0 /ray.xとします。

flaot distance = min( (-2) / ray.x, factor.y / ray.y);

他にも下記のような記述方法もあります。

factor.x = ray.x > 0 ? 1 : -1;
flaot distance = min( factor.x - 1 / ray.x , factor.y / ray.y);

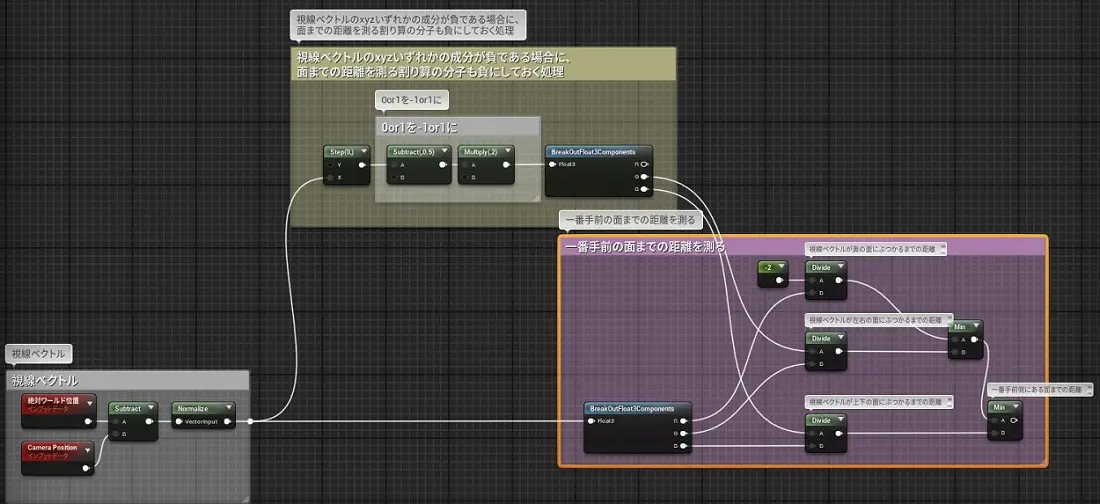
以上の対応を入れたら、Houdiniでは下記のようになります。いい感じになってきましたね！

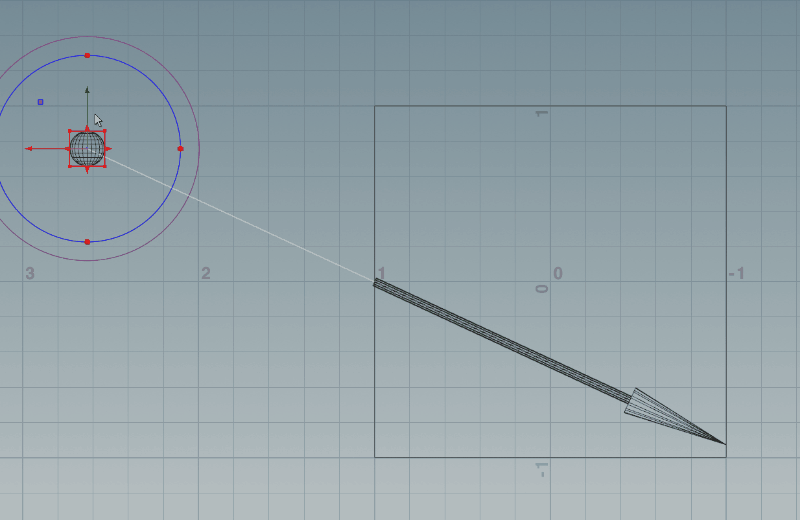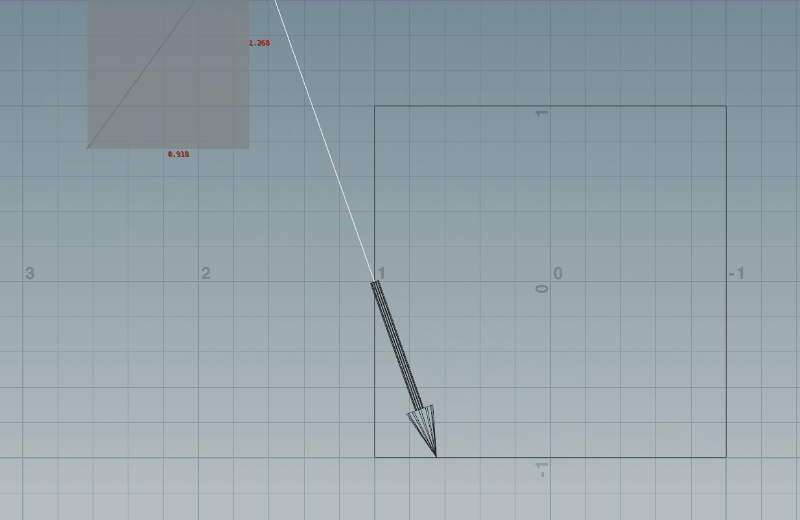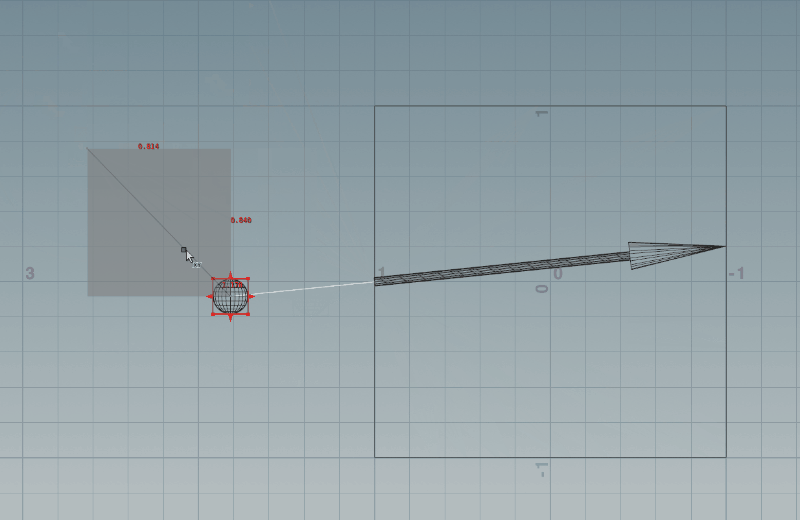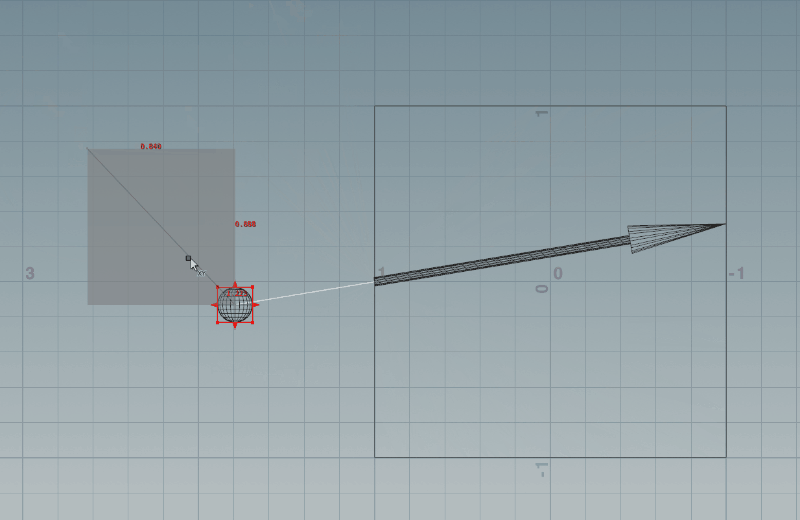
続きは後編で！

だいぶ長くなってきたので、前編はここまでとしたいと思います。
後編も同時に公開されていますので、是非チェックしてください！