
こんにちは、プログラム課のTです。
一昨年の新卒採用連動企画第2回で記事を書きましたが、再び機会がやってまいりました。
前回は2D流体エフェクトに関して触れましたが、あれから技術研究として3Dでの粒子流体シミュレーションに関して調査と実装、社内勉強会を開催する機会がありました。
というわけで今回は粒子流体の計算に関して簡単ですが説明をしてみたいと思います。
格子法と粒子法
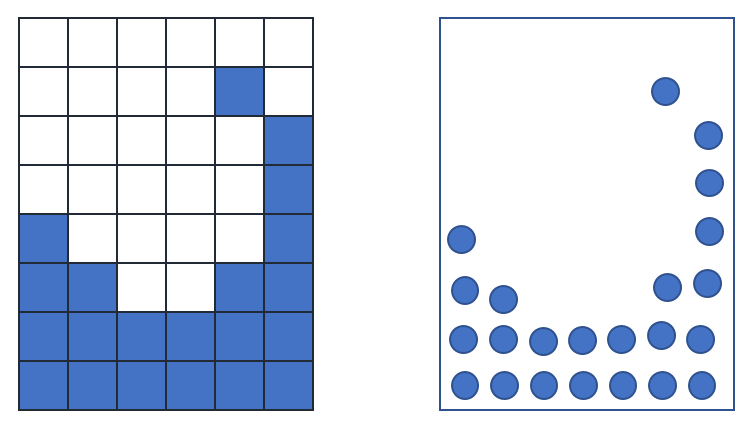
流体シミュレーションのアプローチには大きく分けて「格子法」と「粒子法」があります。格子法では空間を格子状に細かく分割し、一つ一つの立方体(3Dの場合)に流体が詰まっていると考えます。そして隣り合った立方体との流体の行き来を計算することで流体をシミュレートします。Euler的と表現されますね。
それに対して粒子法では流体を細かい粒子の集まりとして扱い、たくさんの粒子が近くの粒子と影響しあって流れていくことでシミュレーションが進みます。こちらはLagrange的などと呼ばれます。今回は粒子法の一種であるSPHについて説明します。
SPH(Smoothed Particle Hydrodynamics)
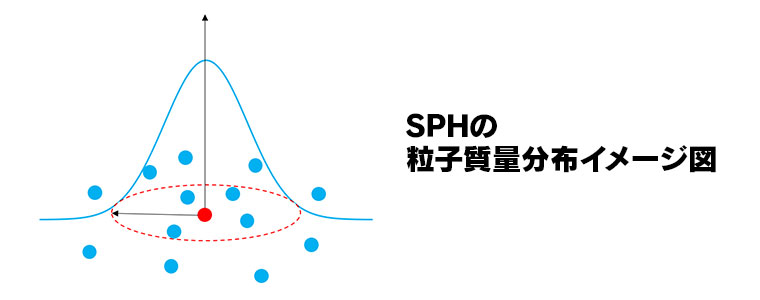
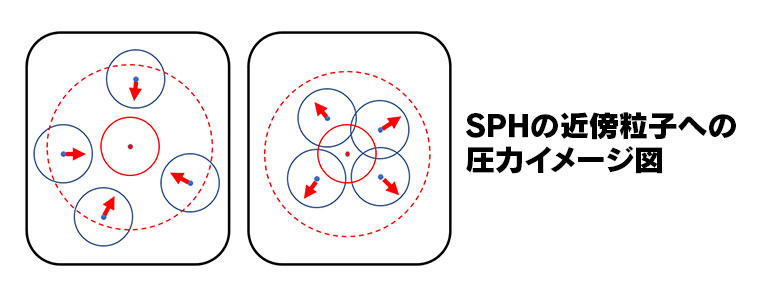
SPHは元々天体や銀河の動きを計算するためのモデルだったそうですが、リアルタイムの流体シミュレーションにも応用されている手法です。この手法では、粒子は中心座標と半径を持っていますが、硬い球として存在するのではなく、中心を頂点とする山の形に質量が分布していると考えます。そして半径内にあるほかの粒子の質量分布を足し合わせたものを密度とします。この密度が基準よりも高ければ半径内の他粒子を遠ざけ、低ければ引き寄せるような圧力を計算することで流体が潰れたり拡散しないようにしています。
さらに流体は粘性が高いとドロドロした動きになりますが、この粘性による力も半径内の他の粒子との相互作用で計算されます。
具体的な圧力、粘性の計算はNavier-Stokes方程式を粒子に関して離散化して計算しますが、紙面の都合により詳細は論文などを参照してください
近傍探索
ここまでの説明で密度、圧力、粘性の計算のためにそれぞれの粒子が自分の近くの粒子を参照する必要があることに触れましたが、リアルタイムで計算するにあたり最も重要と思われるのがこの近傍探索になります。当たり判定の高速化では八分木やBVHなどが使われることがあるかと思いますが、粒子法では数万オーダーの粒子に関して毎フレーム近傍情報を構築する必要があるため、構築コストが小さい方法が求められます。
そこで計算対象の粒子がすべて同じ半径を持っているものとして、1辺が粒子半径と同じ長さの等間隔格子を採用します。粒子がどのセルに所属するかは座標を粒子半径で割って整数化するだけなので高速ですし、近傍探索に関しても所属セルとその隣接セルに含まれる粒子を探索するだけですので実装もシンプルです。
GPGPUによる高速化

粒子法は大量の粒子を扱うため、リアルタイムで動作させるにはGPUで並列計算をするのが必要かと思われます。幸い近年ではComputeShader等のおかげでGPGPUの敷居が低くなっていますので、調べてみると面白いかもしれません。
流体シミュレーションに関して社内勉強会で発表する機会があり、その関係で今回の記事を書くことになりましたが如何だったでしょうか。トイロジックではグラフィックスやゲームエンジン、コーディング技術、将又今回の流体などの様々な勉強会が開催されています。技術交流が活発なトイロジックは皆さまのエントリーをお待ちしています。